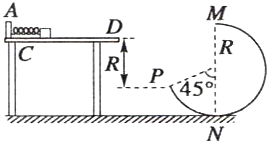
如图所示,水平桌面上有一轻弹簧,左端固定在A点.水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R.用质量m=0.2kg的物块将弹簧缓慢压缩到C点,弹簧和物块具有的弹性势能Ep=7.2J,释放后物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道g=10m/s2,求:
(1)DP间的水平距离;
(2)判断m能否沿圆轨道到达M点;
(3)释放后m运动过程中克服摩擦力做的功.
(1)设物块由D点以初速度vD做平抛运动,落到P点时其竖起速度为vy,有vy2=2gR
而
=tan45°,解得vD=4m/svy vD
设物块做平抛运动的时间为t,水平位移为x,有R=
gt2,x=vDt,解得x=1.6m1 2
(2)若物块能沿轨道到达M点,设其速度为vM,有
mgR=2 2
mvD2-1 2
mvM21 2
解得vM≈2.2m/s<
≈2.8m/sgR
即物块不能到达M点.
(3)设m在桌面上运动过程中克服摩擦力做功为Wf,有Ep-Wf=
mvD21 2
解得Wf=5.6J
答:(1)DP间的水平距离1.6m;
(2)m2不能否沿圆轨道到达M点;
(3)m2释放后在桌面上运动的过程中克服摩擦力做的功为5.6J.

 键的数目
键的数目