如图甲所示,一长为4m的粗糙水平面OA与倾角为300的足够长光滑斜面AB在A处用一小段光滑圆弧相连,一质量为m的滑块从O处由静止开始受一水平力作用(力向右为正),F只在水平面上按图乙所示的规律变化,O点左侧有一水池,O点高出水面1.5m,滑块与水平面间的动摩擦因数为μ=0.25,g=10m/s2,求:
(1)滑块滑到A的速度大小VA
(2)滑块能冲上斜面的长度S
(3)要使滑块返回O点(OA段水平拉力已撤除)后不落入水中,水池的最大宽度L
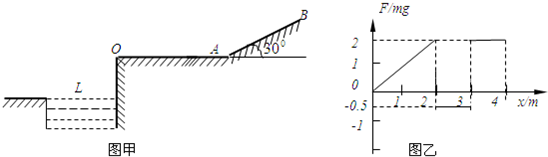
(1)由题图乙知,在前2 m内,力F1做的功为W1=
×2×2mg=2mg,1 2
在第3 m内,力F2做的功为W1=-1×0.5mg=-0.5mg;
在第4 m内力F3做的功为W3=1×2mg=2mg.
滑动摩擦力f做的功为:Wf=-μmgx=-mg.
对OA过程由动能定理列式得
W1+W2+W3+Wf=
mvA2-01 2
解得VA=5
m/s.2
(2)冲上斜面的过程,由动能定理得
-mg•L•sin30°=0-
mvA2,1 2
所以冲上斜面AB的长度L=5 m.
(3)从A返回到O点的过程中运用动能定理得:
mv02-1 2
mvA2=Wf1 2
解得:v0=
m/s30
从O点抛出后做平抛运动,竖直方向做自由落体运动,t=
=2h g
s=2×1.5 10
s30 10
水平方向做匀速直线运动,L=v0t=
×30
m=3m30 10
答:(1)滑块到A处的速度大小为5
m/s.2
(2)不计滑块在A处的速率变化,滑块冲上斜面的长度是5m.
(3)要使滑块返回O点(OA段水平拉力已撤除)后不落入水中,水池的最大宽度L为3m.
