问题
问答题
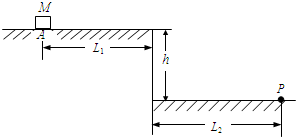
如图所示,在平台的A点处静止一质量为M=0.8kg的木块,平台离地面高h=1.25m,木块离平台的右边缘L1=1.5m.现用一个水平向右、大小等于10N的力F作用在木块上,使木块向右运动;当木块的位移等于1m时,撤去力F,木块继续运动,并落到地面上的P点,测得P点离平台的水平距离L2=2m.
(1)求木块与平台之间的动摩擦因数;
(2)重新把木块静置在A点,用一铅弹以水平向右的速度v0打入木块,使木块向右运动.若铅弹质量m=0.02kg,铅弹打入木块后在很短时间内停在木块中,木块与平台之间的动摩擦因数保持不变.则要使木块也能落到P点,v0必须多大?( g=10m/s2)
答案
(1)设木块与平台之间的动摩擦因数为μ,木块离开平台时的速度为v2,从平台抛出落到地面所需时间为t,铅弹打入木块后相对木块静止时的速度为v1,则有
FS-μMgL1=
M1 2
①v 22
h=
gt2 ②1 2
L2=v2t ③
联立②、③式解得:v2=4m/s
代入①式,解得 μ=0.3
(2)铅弹打入木块的过程满足动量守恒定律:
mv0=(M+m)v1 ⑤
铅弹打入木块后,木块和铅弹以速度v1从A点滑到平台边缘的过程,由动能定理有:
μ(M+m)gL1=
(M+m)1 2
-v 21
(M+m)1 2
⑥v 22
把已知数值代入⑤、⑥式,解得:v0=205m/s
答:
(1)木块与平台之间的动摩擦因数是0.3;
(2)要使木块也能落到P点,v0必须205m/s.
