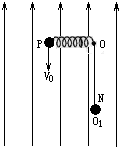
如图所示，轻弹簧一端连于固定点O，可在竖直平面内自由转动，另一端连接一带电小球P，其质量m=2×10-2 kg，电荷量q=0.2C．将弹簧拉至水平后，以初速度V0=20m/s竖直向下射出小球P，小球P到达O点的正下方O1点时速度恰好水平，其大小V=15m/s．若O、O1相距R=1.5m，小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰．碰后瞬间，小球P脱离弹簧，小球N脱离细绳，同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场．此后，小球P在竖直平面内做半径r=0.5m的圆周运动．小球P、N均可视为质点，小球P的电荷量保持不变，不计空气阻力，取g=10m/s2．那么，
（1）弹簧从水平摆至竖直位置的过程中，其弹力做功为多少？
（2）请通过计算并比较相关物理量，判断小球P、N碰撞后能否在某一时刻具有相同的速度．
（3）若题中各量为变量，在保证小球P、N碰撞后某一时刻具有相同速度的前提下，请推导出r的表达式（要求用B、q、m、θ表示，其中θ为小球N的运动速度与水平方向的夹角）．
（1）设弹簧的弹力做功为W，有：mgR+W=
mv2-1 2
m1 2
①v 20
代入数据，得：W=-2.05J ②
（2）由题给条件知，N碰后作平抛运动，P所受电场力和重力平衡，P带正电荷．设P、N碰后的速度大小分别为v1和V，
并令水平向右为正方向，有：mv=±mv1+MV③
而：v1=
④Bqr m
若P、N碰后速度同向时，计算可得V＜v1，这种碰撞不能实现．P、N碰后瞬时必为反向运动．有：V=
⑤mv+Bqr M
P、N速度相同时，N经过的时间为tN，P经过的时间为tP．设此时N的速度V1的方向与水平方向的夹角为θ，
有：cosθ=
=V V1
⑥V v1
gtN=V1sinθ=v1sinθ⑦
代入数据，得：tN=
s⑧3 4
对小球P，其圆周运动的周期为T，有：T=
⑨2πm Bq
经计算得：tN＜T，
P经过tP时，对应的圆心角为α，有：tP=
T⑩α 2π
当B的方向垂直纸面朝外时，P、N的速度相同，如图可知，有：α1=π+θ
联立相关方程得：tP1=
s2π 15
比较得，tN≠tP1，在此情况下，P、N的速度在同一时刻不可能相同．
当B的方向垂直纸面朝里时，P、N的速度相同，同样由图，有：a2=π-θ，
同上得：tP2=
，π 15
比较得，tN≠tp2，在此情况下，P、N的速度在同一时刻也不可能相同．
（3）当B的方向垂直纸面朝外时，设在t时刻P、N的速度相同，tN=tP=t，
再联立④⑦⑨⑩解得：r=
(n=0，1，2…)[(2n+1)π+θ]m2g B2q2sinθ
当B的方向垂直纸面朝里时，设在t时刻P、N的速度相同tN=tP=t，
同理得：r=
，(π-θ)m2g B2q2sinθ
考虑圆周运动的周期性，有：r=
(n=0，1，2…)（给定的B、q、r、m、θ等物理量决定n的取值）．[(2n+1)π+θ]m2g B2q2sinθ
答：（1）弹簧从水平摆至竖直位置的过程中，其弹力做功为-2.05J；（2）小球P、N碰撞后不能在某一时刻具有相同的速度；（3）r=
(n=0，1，2…)（给定的B、q、r、m、θ等物理量决定n的取值）．[(2n+1)π+θ]m2g B2q2sinθ
5Z(g) ΔH<0，在某温度时X的浓度随时间变化的曲线：