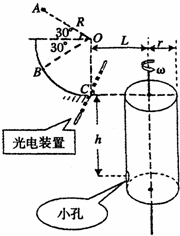
如图所示,半径R=0.80m的
光滑圆弧轨道竖直固定,过最低点的半径OC处于竖直位置.其右方有底面半径r=0.2m的转筒,转筒顶端与C等高,下部有一小孔,距顶端h=0.8m.转筒的轴线与圆弧轨道在同一竖直平面内,开始时小孔也在这一平面内的图示位置.今让一质量m=0.1kg的小物块自A点由静止开始下落后打在圆弧轨道上的B点,但未反弹,在瞬问碰撞过程中,小物块沿半径方向的分速度立刻减为0,而沿切线方向的分速度不变.此后,小物块沿圆弧轨道滑下,到达C点时触动光电装置,使转筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔.已知A、B到圆心O的距离均为R,与水平方向的夹角均为θ=30°,不计空气阻力,g取l0m/s2.求:1 4
(1)小物块到达C点时对轨道的压力大小 FC;
(2)转筒轴线距C点的距离L;
(3)转筒转动的角速度ω.
(1)小物块由A→B的过程中,
2mgRsin30°=
mvB21 2
vB=4m/s
在瞬间碰撞过程中,小物块沿半径方向的分速度立刻减为0,沿切线方向的分速度不变.
则碰撞后瞬间小物块速度
vB'=vBcos30°=2
m/s 3
小物块由B→C的过程中根据动能定理得:
mgR(1-sin30°)=
mvC2-1 2
mvB'21 2
vC=
m/s 20
小物块在C点,根据向心力公式得:
F-mg=vC2 R
解得:F=3.5N
所以由牛顿第三定律知,小物块对轨道压力的大小FC=3.5N
(2)小球由C到小孔做平抛运动
h=
gt2 1 2
解得:t=0.4s
所以L=vCt+r=(0.8
+0.2)m 5
(3)小物块最终正好进入小孔,所以在小球做平抛运动的时间里,转筒正好转了n圈,
即t=nT=n
(n=1,2,3…).2π ω
解得:ω=
=5nπrad/s (n=1,2,3…).2nπ t
答:(1)小物块到达C点时对轨道的压力大小为3.5N;
(2)转筒轴线距C点的距离L为(0.8
+0.2)m;5
(3)转筒转动的角速度ω为5nπrad/s (n=1,2,3…).
