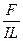问题
多选题
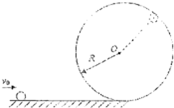
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
A.初速度v0应满足
<v0<2gR 5gR
B.小球脱离轨道后做平抛运动
C.小球脱离轨道时的速度大小为v=
-2gRv 20 3
D.在脱离轨道之前小球对轨道的压力大小保持不变
答案
A、若小球恰好运动到与圆心等高处,根据动能定理得:
0-
mv02=-mgR1 2
解得:v0=2gR
若小球恰好能运动到最高点,此时重力提供向心力,根据向心力公式得:
mg=mv2 R
解得:v=gR
根据动能定理得:
mv2-1 2
mv02=-2mgR1 2
解得:v0=5gR
所以要使小球在图中虚线位置脱离轨道,则初速度v0应满足
<v0<2gR
,故A正确;5gR
B、小球脱离后做斜抛运动,故B错误;
C、脱落的瞬间轨道对小球的压力恰好为零,重力的指向圆心的分量提供向心力,则有:
mgcosθ=mv2 R
mv2-1 2
mv02=-mg(R+Rcosθ)1 2
解得:v=
,故C正确;
-2gRv 20 3
D、在最低点有:N-mg=m
,此时速度最大,所以此时N也是最大的,故D错误.v2 R
故选AC