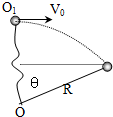
一质量为m的很小的球,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的.今把小球从O点的正上方离O点的距离为R的O1点以水平的速度V0=抛出,如图所示.以O点为零势能面,试求:
(1)小球在O1点的机械能为多大?
(2)轻绳刚伸直(绳子突然拉紧会使平行于绳子的速度突变为零)时,绳与竖直方向的夹角θ为多少?
(3)当小球到达O点的正下方时,所受的合外力是多大?
(1)小球在O1点的机械能等于该点的动能加重力势能,即E=m+mgR=.
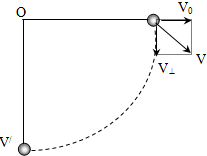
(2)第一过程:质点做平抛运动.设绳即将伸直时,绳与竖直方向的夹角为θ,如图所示则V0t=Rsinθ,gt2=R-Rcosθ,其中V0=
联立解得θ=,t=.
(3)绳绷直过程.绳棚直时,绳刚好水平,如图所示,由于绳不可伸长,故绳绷直时,V0损失,质点仅有速度V⊥,且V⊥=gt=.
小球在竖直平面内做圆周运动.设质点到达O点正下方时,速度为V′,根据机械能守恒守律有:mV/2=mV⊥2+mg•R
设最低点合外力为F,则F=m,联立解得:F=mg
答:(1)小球在O1点的机械能为;
(2)轻绳刚伸直(绳子突然拉紧会使平行于绳子的速度突变为零)时,绳与竖直方向的夹角θ为;
(3)当小球到达O点的正下方时,所受的合外力是mg.