问题
解答题
如何证明三角形的内角和为180°？
答案
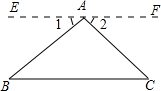
证明：如图所示，在△ABC中，过A引EF∥BC，
∵EF∥BC，
∴∠B=∠1，∠C=∠2（内错角相等）．
∵∠1+∠BAC+∠2=180°，
∴∠A+∠B+∠C=180°．
即三角形的内角和为180°．
搜题请搜索小程序“爱下问搜题”
如何证明三角形的内角和为180°？
证明：如图所示，在△ABC中，过A引EF∥BC，
∵EF∥BC，
∴∠B=∠1，∠C=∠2（内错角相等）．
∵∠1+∠BAC+∠2=180°，
∴∠A+∠B+∠C=180°．
即三角形的内角和为180°．