问题
选择题
如图所示，有一光滑的半径可变的
圆形轨道处于竖直平面内，圆心O点离地高度为H．现调节轨道半径，让一可视为质点的小球a从与O点等高的轨道最高点由静止沿轨道下落，使小球离开轨道后运动的水平位移S最大，则小球脱离轨道最低点时的速度大小应为（ ）1 4
A．gH
B．gH 3
C．2gH 3
D．4gH 3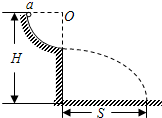 
答案
设圆形轨道的半径为r，则小球做平抛运动的高度为H-r，
小球从最高点运动到轨道最低点的过程中，运用动能定理得：
mgr=
mv21 2
解得：v=2gr
小球从轨道最低点抛出后做平抛运动，则有
t=2(H-r) g
水平位移S=vt=2(H-r) g
=2gr 4(H-r)r
当H-r=r时，S取最大值，即r=H 2
所以v=
=2gr gH
故选A
