如图所示，一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平

问题问答题

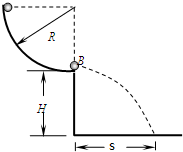
如图所示，一个半径R=0.80m的四分之一光滑圆形轨道固定在竖直平面内，底端切线水平，距地面高度H=1.25m．在轨道底端放置一个质量m_B=0.30kg的小球B．另一质量m_A=0.10kg的小球A（两球均视为质点）由圆形轨道顶端无初速释放，运动到轨道底端与球B发生正碰，碰后球B水平飞出，其落到水平地面时的水平位移S=0.80m．忽略空气阻力，重力加速度g取10m/s²，求：

（1）A、B碰前瞬间，A球对轨道压力大小和方向

（2）B球离开圆形轨道时的速度大小．

答案

（1）A由光滑轨道滑下，机械能守恒，设小球A滚到轨道下端时速度为v₁，

则mAgR=

mAv12

在底端，由牛顿第二定律：FN-mAg=mA

代入数据解得：F_N=3N

由牛顿第三定律知，球A对轨道的压力大小为3N，方向竖直向下．

（2）物块B离开轨道最低点后作平抛运动，设其飞行时间为t，离开轨道下端时的速度为v₂，则

gt2

s=v₂t

代入数据解得：v₂=1.6m/s

答：（1）A、B碰前瞬间，A球对轨道压力大小为3N，方向竖直向下；

（2）B球离开圆形轨道时的速度大小为1.6m/s．