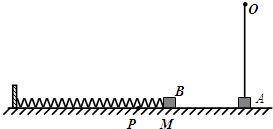
如图所示,水平地面M点左侧粗糙,右侧光滑.整个空间有一场强大小E1=1×103N/C、方向竖直向下的匀强电场.质量mA=0.04kg的不带电小物块A用长为R=5m不可伸长的绝缘轻质细绳拴于O点,静止时与地面刚好接触.带正电的小物块B与左端固定在墙上的绝缘轻弹簧接触但不粘连,B的质量mB=0.02kg,带电量为q=+2×10-4 C,与M左侧地面间动摩擦因数μ=0.5.现用水平向左的推力将B由M点(弹簧原长处)缓慢推至P点(弹簧仍在弹性限度内),推力做功W=2.65J,MP之间的距离为L=50cm.撤去推力,B向右运动,随后与A发生正碰并瞬间成为一个整体C(A、B、C均可视为质点).已知碰撞前后电荷量保持不变,碰后C的速度为碰前B速度的
.碰后立即把匀强电场方向变为竖直向上,场强大小变为E2=6×103N/C.(取g=10m/s2)求:1 3
(1)B与A碰撞过程中损失的机械能.
(2)碰后C是否立即做圆周运动?如果是,求C运动到最高点时绳的拉力大小;如果不是,则C运动到什么位置时绳子再次绷紧?
(1)小球B在PM间运动时受到的摩擦力为f=μ(mBg+E1q)
由功能关系得,弹簧具有的最大弹性势能 EP=W-μ(mBg+E1q)l=2.45J
设小球B运动到M点时速度为vB,由功能关系得
EP-μ(mBg+E1q)L=
mBvB2 1 2
解得 vB=15m/s
两球碰后结合为C,则C的速度为vC=
vB=5m/s 1 3
B与A碰撞过程中损失的机械能△E=
mBvB2-1 2
(mA+mB)vC2=1.5J.1 2
故B与A碰撞过程中损失的机械能为1.5J.
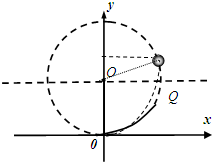
(2)电场变化后,因E2q-mCg=0.6N
mc
=0.3N 所以C不能做圆周运动,而是做类平抛运动.vc2 R
设经过时间t绳子在Q(x,y)处绷紧,由运动学规律得
x=vct
y=
at21 2
a=
=10m/s2E2q-mcg mc
x2+(y-R)2=R2
可得 t=1s
x=y=R=5m
即:绳子绷紧时恰好位于水平位置.
