如图所示，圆桶底面半径为R，在上部有个入口A，在A的正下方h处有

问题填空题

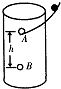
如图所示，圆桶底面半径为R，在上部有个入口A，在A的正下方h处有个出口B，在A处沿切线方向有一斜槽，一个小球恰能沿水平方向进入入口A后，沿光滑桶壁运动，要使小球由出口B飞出桶外，那么小球进入A时速度v必须满足______．

答案

小球从入口A进入桶内以后，在竖直方向只受重力作用，且竖直方向初速度为零，

故小球在竖直方向做自由落体运动，由h=

gt^{2
从A运动到B的时间为：t=
2h
g
----------①
小球在水平方向以速率v做匀速圆周运动，设它从A到B共运动了n圈，则：
　 vt=n•2πR，（n=1、2、3…）---------------②
联立①②解得：V=2πnR
g
2h
（n=1，2，3，…）
　此即为小球进入A时速度v所必须满足的条件．
故答案为：2πnR
g
2h
（n=1，2，3，…）．}