问题
问答题
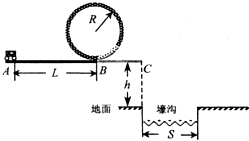
某校物理兴趣小组举行了一场遥控赛车表演赛.赛车走过的路径如图所示.第一次表演,赛车从A点出发,以额定功率P=5W沿水平直轨道AB运动一段时间后关闭电源,再由B点进入半径为R的光滑竖直圆轨道,赛车恰好能通过竖直圆轨道最高点,然后沿圆轨道运动,进入另一条与AB轨道等高的光滑平直轨道,并从C点飞出.已知赛车质量m=lkg,可视为质点,进入竖直圆轨道前受到阻力大小恒定为f=0.3N.在运动中受到的其他阻力均可不计.g=10m/s2.已知A、B间距离L=10m,圆轨道半径R=0.18m,水平直轨道ABC与地面之间的高度差是h=1.8m,壕沟宽S=2.4m.C点在壕沟左边缘的正上方.求:
(1)第一次表演时,赛车到达B点的速度多大?
(2)第二次表演,要使赛车越过壕沟,电动机至少要工作多长时间?
答案
(1)小球恰好到最高点,
由动能定理得:mg=m
,v2 R
从B到最高点过程中,由动能定理可得:
-2mgR=
mv2-1 2
mvB2,1 2
解得:vB=3m/s;
(2)在赛车越过战壕的过程中,做平抛运动,
在竖直方向上:h=
gt2,1 2
在水平方向上:s=vCt,
解得:vC=4m/s,
从A到C过程中,由动能定理得:
Pt-fL=
mvC2-0,1 2
解得:t=2.2s;
答:(1)赛车到达B点的速度为3m/s.
(2)电动机至少要工作2.2s.
