问题
问答题
如图所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h=1.4m、宽L=1.2m的长方体障碍物,为了不触及这个障碍物,他必须在距水平地面高度H=3.2m的A点沿水平方向跳起离开斜面.已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10m/s2.(已知sin53°=0.8,cos53°=0.6)求:
(1)若运动员不触及障碍物,他从A点起跳后到落至水平面的过程所经历的时间;
(2)运动员为了不触及障碍物,他从A点跳离斜面的最小速度.
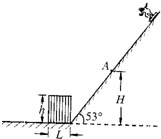
答案
(1)由平抛规律:H=
gt2得:t=1 2 2H g
代入数据:t=0.8s
(2)设运动员刚好不触及障碍物的情况下,在A点的水平速度为v0
则y=H-h=1.8m
x=Hcotθ+L=3.6m
由平抛运动规律得:
X=v0t
Y=
gt21 2
代入数据得v0=6.0m/s.
答:(1)从A点起跳后到落至水平面的过程所经历的时间为0.8s.
(2)跳离斜面的最小速度6.0m/s.
