问题
问答题
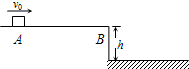
如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.5.滑块运动到平台边缘的B点后水平飞出.已知AB=2.7m.不计空气阻力,g取10m/s2,求:
(1)滑块从B点飞出时的速度大小;
(2)滑块落地点到平台边缘的水平距离;
(3)滑块落地前瞬间的速度与水平方向的夹角(结果可直接用三角函数表示).
答案
(1)设滑块到达B点的速度为vB,由动能定理得:
-μmgs=
nvB2-1 2
mv021 2
故vB=
=v02-2μgs
m/s=3m/s62- 2×0.5×10×2.7
(2)由平抛运动规律,竖直方向做自由落体运动,则
h=
g t21 2
所以t=
=0.4s2h g
水平方向做匀速直线运动,x=vBt=3×0.4m=1.2m
即滑块落地点到平台边缘的水平距离为1.2m;
(3)落地前瞬间竖直速度为:
vy=gt=10×0.4m/s=4m/s
水平方向的速度为vB=3m/s,设速度与水平方向的夹角为α,
则 tanα=
=vy vB
.4 3
答:(1)滑块从B点飞出时的速度大小为3m/s;(2)滑块落地点到平台边缘的水平距离为1.2m;(3)滑块落地前瞬间的速度与水平方向的夹角为tanα=
.4 3
