问题
解答题
证明:两条平行线的同旁内角的角平分线互相垂直.
答案
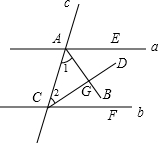
如图所示,直线a,b被直线c所截,且a∥b,直线AB平分∠CAE,直线CD平分∠ACF,AB,CD相交于点G.
求证:AB⊥CD.
证明:∵a∥b,
∴∠CAE+∠ACF=180°.
又AB平分∠CAE,CD平分∠ACF,
所以∠1=
∠CAE,∠2=1 2
∠ACF.1 2
所以∠1+∠2=
∠CAE+1 2
∠ACF1 2
=
(∠CAE+∠ACF)=1 2
×180°=90°.1 2
又∵△ACG的内角和为180°,
∴∠AGC=180°-(∠1+∠2)=180°-90°=90°.
∴AB⊥CD.