如图所示，已知倾角为θ=45°、高为h的斜面固定在水平地面上．一

问题问答题

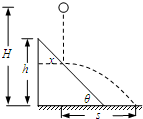
如图所示，已知倾角为θ=45°、高为h的斜面固定在水平地面上．一小球从高为H（h＜H＜

h）处自由下落，

与斜面做无能量损失的碰撞后水平抛出．小球自由下落的落点距斜面左侧的水平距离x满足一定条件时，小球能直接落到水平地面上．

（1）求小球落到地面上的速度大小；

（2）求要使小球做平抛运动后能直接落到水平地面上，x应满足的条件；

（3）在满足（2）的条件下，求小球运动的最长时间．

答案

（1）设小球落到底面的速度为v，根据机械能守恒得：

mgH=

mv2，

得：v=

2gH

（2）小球做自由落体的末速度为：v0=

2g(H-h+x)

小球做平抛运动的时间为：t=

2(h-x)

s=2

(H-h+x)•(h-x)

由s＞h-x

解得：h-

H＜x＜h

（3）t总=

2(H-h+x)

2(h-x)

t总2=

(H-h+x)(h-x)

当H-h+x=h-x，即x=h-

时，小球运动时间最长，

x=h-

，符合（2）的条件

代入得：tm=2

答：

（1）小球落到地面上的速度大小为

2gH

；

（2）要使小球做平抛运动后能直接落到水平地面上，x应满足的条件为h-

H＜x＜h；

（3）在满足（2）的条件下，小球运动的最长时间为2

．