问题
单项选择题
若函数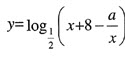 在(1,+∞)上单调递减,则实数a的取值范围为()。
在(1,+∞)上单调递减,则实数a的取值范围为()。
A.[-1,8]
B.[-1,9]
C.(-1,8)
D.(-1,9)
答案
参考答案:B
解析:
设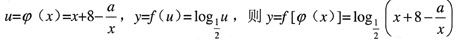
由函数的解析式有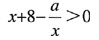
因为x>1,故a<x2+8x
因为x2+8x=(x+4)2-16
故当x>1时,x2+8x>9,故由①得a≤9
因为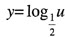 是减函数,又已知
是减函数,又已知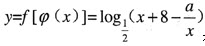 在(1,+∞)上是减函数,
在(1,+∞)上是减函数,
设1<x1<x2,则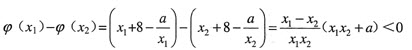
因为 ,故x1x2+a>0,a>-x1x2 ②
,故x1x2+a>0,a>-x1x2 ②
因为-x1x2<-1,故由②得a≥-1
综上,实a的取值范围为-1≤a≤9
故正确答案为B。
