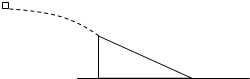
如图所示,一质量为1kg的物体在空中从某高度以4m/s的水平初速度开始做平抛运动,刚好沿斜面方向落在一个高6米倾斜角为
37°的直角三角形上,三角形固定在水平面上,物体与斜面间的动摩擦因数μ=0.5.求:
(1)物体落在斜面上的速度大小;
(2)物体出发点距斜面顶端的高度h;
(3)物体到达斜面底端时的速度大小.
(1)据题:物体速度刚好沿斜面方向时,速度与水平方向的夹角为37°,则得:
v=
=v0 cos37°
m/s=5m/s4 0.8
(2)物体落在斜面上时竖直方向的分速度 vy=v0tan37°=4×
m/s=3m/s3 4
平抛运动的时间 t=
=vy g
s=0.3s3 10
则物体出发点距斜面顶端的高度 h=
gt2=1 2
×10×0.32m=0.45m1 2
(3)物体沿斜面运动的过程,根据动能定理得:
mgH-μmgcos37°•
=H sin37°
mv′2-1 2
mv21 2
代入得:10×6-0.5×10×0.8×
=6 0.6
v′2-1 2
×521 2
则得:v′=7m/s
答:
(1)物体落在斜面上的速度大小为5m/s;
(2)物体出发点距斜面顶端的高度h为0.45m;
(3)物体到达斜面底端时的速度大小为7m/s.

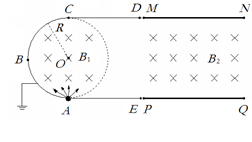
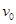 大小、方向如何?
大小、方向如何?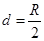 的电子在圆形磁场中运动了多长时间?
的电子在圆形磁场中运动了多长时间?