参考答案：D

解析：

函数y=2^x的图像向右平移1个单位得y=2^x-1的图像，再向下平移1个单位得y=2^x-1-1的图像，再将x轴下方的部分翻折到x轴上方得y=|2^x-1-1|的图像(见右图)。

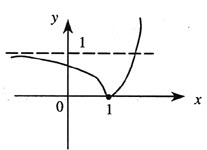
由于在(-∞,1)上f(x)递减，故a、b、c不能同时在(-∞, 1]上；同理，a、b、c也不能同时在[1,+∞)上，所以有a＜ 1且c＞1。

从而有2^a-1＜1，2^c-1＞1

故f(a)=1-2^a-1，f(c)=2^c-1-1

因为，f(a)＞f(c)

即1-2^a-1＞2^c-1-1

故2^a+2^c＜4

故正确答案为D。