如图所示,半径为R,内径很小的光滑半圆细管竖直放置,一质量为m的小球A以某一速度从下端管口进入,并以速度v1通过最高点C时与管壁之间的弹力大小为0.6mg,另一质量也为m小球B以某一速度从下端管口进入,并以速度v2通过最高点C时与管壁之间的弹力大小为0.3mg,且v1>v2,g=10m/s2.当A、B两球落地时,落地点与下端管口之间的水平距离xB、xA之比可能为( )
A.
=xB xA 7 2
B.
=xB xA 13 2
C.
=xB xA 7 4
D.xB xA= 13 4
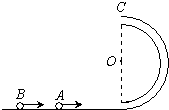
以A球为对象,设其到达最高点时的速度为vA,根据向心力公式有:
FA+mg=mv 2A R
又FA=0.6mg
代入解得:vA=1.6gR
以B球为对象,设其到达最高点时的速度为vB,有两种情况:
若管壁对B球的弹力方向向上,根据向心力公式有
mg-FB=mv 2B R
又FB=0.3mg
所以得:vB=0.7gR
两球脱离轨道的最高点后均做平抛运动,高度相等,运动时间相等,由x=v0t可得:
两球的水平位移之比为:
=xB xA
=vB vA
;7 4
若管壁对B球的弹力方向向下,根据向心力公式有
mg+FB=mv 2B R
得:vB=1.3gR
同理可得:
=xB xA 13 4
故选:CD.
