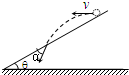
如图所示，从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出，小球均落在斜面上，当抛出的速度为v1时，小球到达斜面时速度方向与斜面的夹角为α1；当抛出速度为v2时，小球到达斜面时速度方向与斜面的夹角为α2，则（ ）
A．当v1＞v2时，α1＞α2
B．当v1＞v2时，α1＜α2
C．无论v1、v2关系如何，均有α1=α2
D．α1、α2的关系与斜面的倾角θ无关
设当将小球以初速度v0平抛时，在斜面上的落点与抛出点的间距为L，则由平抛运动的规律得Lcosθ=v0t，Lsinθ=
gt2，整理得1 2
=v0 gt
cotθ，若设落到斜面上时小球速度方向与竖直方向的夹角为r，则有tanr=1 2
=v0 gt
cotθ是恒量，与初速度无关，α=1 2
-θ-r也是恒量，可知到达斜面时速度方向与斜面的夹角不变，α1一定等于α2．故C正确，A、B、D错误．π 2
故选：C．
（1）两组图片分别反映了怎样的经济体制？它们最大的区别是什么？
________________________________________________________________________________________________________________________________________________________________
（2）从第一组图片到第二组图片的转变，党和政府采取了哪些重大的措施？
________________________________________________________________________________________________________________________________________________________________
（3）根据两组图片谈谈你的认识。
________________________________________________________________________________________________________________________________________________________________