问题
单项选择题
设集合A={x|2lgx=lg（8x-15），x∈R），B={x|cos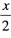
＞0，x∈R}，则A∩B的元素个数为（）个。
A．1
B．2
C．3
D．4
答案
参考答案：A
解析：
由已知A，得lgx2=lg(8x-15)，
即x2-8x+15=0，解之，x1=3，x2=5
所以A={x|x1=3，x2=5)，又由B，得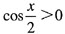
故
4kπ-π＜x＜4kπ+π
故B={x|4kπ-π＜x＜4kπ+π,k∈Z}
(1)当k=0时，-π＜x＜π，得A∩B={x|x=3}。
(2)当k=1时，3π＜x＜5π，得A∩B=φ。
(3)当k=-1时，-5π＜x＜-3π，得A∩B=φ。
故A∩B的元素个数为1个。
故正确答案为A。