问题
问答题
设常数a＞
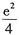，函数f(x)=ex-ax2，证明方程f(x)=0在区间(0，+∞)内有且仅有两个实根．
答案
参考答案：[证明] 在区间(0，+∞)内，f(x)=ex-ax2=0，其等价于φ(x)=
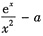=0，即两者实根相同，因此，可讨论φ(x)=0在(0，+∞)内的实根个数．
由于
，
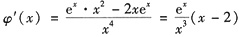令φ’(x)=0，得驻点x=2，列表如下：
| x | (0，2) | 2 | (2，+∞) |
| φ’(x) | - | 0 | + |
| φ(x) | ↘ | 极小 | ↗ |
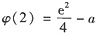，已知
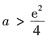，因此φ(2)＜0．显然
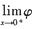(x)=+∞，
，所以φ(x)=0在(0，2)和(2，+∞)上分别有且仅有一个实根，因此φ(x)在(0，+∞)内有且仅有两个实根，即f(x)在(0，+∞)上有且仅有两个实根．
