问题
问答题
设f(x)在[0,1]上具有二阶连续导数,且f(0)=f(1)=0,
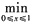 f(x)=-1.证明:
f(x)=-1.证明:
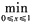 f"(x)≥8.
f"(x)≥8.
答案
参考答案:[证明] 设f(c)=
 f(x)=-1,因为f(0)=f(1)=0,则f(c)是f(x)在区间(0,1)内的极小值,故f’(c)=0,将f(x)按(x-c)的幂展开成二次泰勒多项式,即
f(x)=-1,因为f(0)=f(1)=0,则f(c)是f(x)在区间(0,1)内的极小值,故f’(c)=0,将f(x)按(x-c)的幂展开成二次泰勒多项式,即
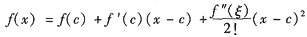 ,
,
在上式中分别令x=0,x=1,得
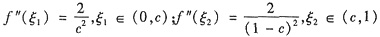 ,
,
若c≤
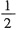 ,则
,则
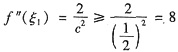 ,
,
若c>
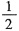 ,则
,则
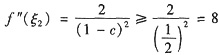
故