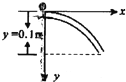
由平抛运动规律容易证明出平抛物体运动轨迹方程为抛物线y=kx2(k为常数).现有内壁光滑的空心玻璃管竖直放置在直角坐标系中,空心玻璃管刚好与抛物线y=2.5x2吻合,在竖直方向的高度为y=0.1m.一直径略小于玻璃管直径的小球(可视为质点)以初速度v=4m/s水平射入玻璃管,与玻璃管碰撞时无能量损失.g=10ms/2.则下列判断正确的是( )
A.从O点以水平初速度v0=m/s的平抛物体,其运动轨迹与玻璃管重合
B.小球射出管口时速度方向与水平方向夹角ϑ=30°
C.小球到达管口的时间是0.1s
D.小球射出管口时速度大小是v=3
A、据题平抛物体的运动轨迹与玻璃管重合时,其轨迹方程为y=2.5x2,将y=0.1m,代入得到 x=0.2m.
由y=gt2,得:t===0.1s,则初速度 v0==m/s=m/s,所以从O点以水平初速度v0=m/s的平抛物体,其运动轨迹与玻璃管重合,故A正确.
B、若小球射出管口时速度方向沿管口的切线方向,由tanθ====1,θ=45°,故B错误.
C、由A项分析可知,做平抛运动的物体运动时间为0.1s,而题中初速度v=4m/s>m/s,所以该小球做的不是平抛运动,运动时间不是0.1s.故C错误.
D、根据机械能守恒得:mgy+mv2=mv′2
得:v′==m/s=3m/s,故D正确.
故选:AD

