问题
单项选择题
已知定义在R上的奇函数f(x)满足f(x+1)=f(x-1)。当x∈(0,1)时f(x)=2x，那么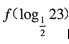
的值为（）。
A.A
B.B
C.C
D.D
答案
参考答案：A
解析：
因为f(x+1)=f(x-1)故f(x)为周期T=2的周期函数
因为x∈(-1,0)时，-x∈(0,1)，故此时f(x)=2-x
又函数f(x)为奇函数，故f(x)=-f(-x)=-2-x
当x∈(-5,-4)时，x+4∈(-1,0)
此时f(x)=f(x+4)=-2-(x+4)
因为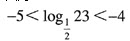
故
故正确答案为A。