问题
单项选择题
设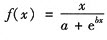 在(-∞,+∞)内连续,但
在(-∞,+∞)内连续,但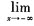 f(x)=0,则常数a,b满足()。
f(x)=0,则常数a,b满足()。
A.a≤0,b<0
B.a≥0,b>0
C.a≤0,b>0
D.a≥0,b<0
答案
参考答案:D
解析:
由题意可知f(x)在(-∞,+∞)内恒成立,因此a+ebx≠0。
由于ebx>0且ebx在(-∞,+∞)内连续,但a+ebx≠0,所以a≥0。
又因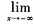 f(x)=0,分子x→∞,故
f(x)=0,分子x→∞,故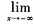 ebx=∞,从而b<0,因此选D。
ebx=∞,从而b<0,因此选D。
设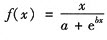 在(-∞,+∞)内连续,但
在(-∞,+∞)内连续,但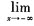 f(x)=0,则常数a,b满足()。
f(x)=0,则常数a,b满足()。
A.a≤0,b<0
B.a≥0,b>0
C.a≤0,b>0
D.a≥0,b<0
参考答案:D
解析:
由题意可知f(x)在(-∞,+∞)内恒成立,因此a+ebx≠0。
由于ebx>0且ebx在(-∞,+∞)内连续,但a+ebx≠0,所以a≥0。
又因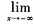 f(x)=0,分子x→∞,故
f(x)=0,分子x→∞,故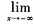 ebx=∞,从而b<0,因此选D。
ebx=∞,从而b<0,因此选D。