问题
填空题
设函数y=f(x)由方程e2x+y-cos(xy)=e-1所确定，则曲线y=f(x)在点(0，1)处的法线方程为______．
答案
参考答案：x-2y+2=0
解析： 在方程e2x+y-cos(xy)=e-1两边对x求导，得
e2x+y(2+y’)+sin(xy)(y+xy’)=0．
将x=0，y=1代入上式，得y’|x=0=-2，则法线斜率为
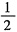，故所求法线方程为y-1=
(x-0)，
即z-2y+2=0．
