问题
问答题
证明不等式
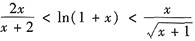对任何x＞0都成立．
答案
参考答案：[证明] 先证明
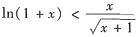，作辅助函数F(x)=
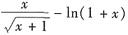，则需证明F(x)＞0成立．
因函数F(x)在区间[0，+∞)上具有连续导数，F(0)=0，且
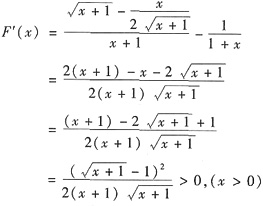
因此F(x)在区间[0，+∞)上单调增加，故当x＞0时，F(x)＞F(0)=0成立，即
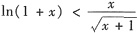成立．
再证
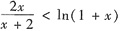，令函数G(x)=
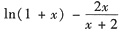，则需证明G(x)＞0成立．
函数G(x)在区间[0，+∞)上具有连续导数，G(0)=0，且
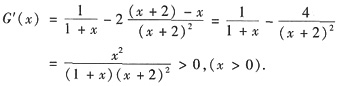
因此G(x)在区间[0，+∞)上单调增加，故当x＞0时，G(x)＞G(0)=0成立，即
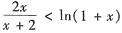成立．
综上所述，命题得证．