参考答案：由已知得

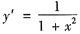，故有
y’(1+x²)=1．
上式两边对x求n阶导数，当n≥3时(1+x²)⁽ⁿ⁾=0，因此由莱布尼茨公式

，
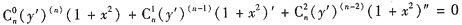即(1+x²)y⁽ⁿ⁺¹⁾+2nxy⁽ⁿ⁾+(n-1)ny^(n-1)=0．
令x=0，得
y⁽ⁿ⁺¹⁾(0)+(n-1)ny^(n-1)(0)=0，
根据该递推关系，则y⁽ⁿ⁾(0)=(1-n)(n-2)y^(n-2)(0)，n≥2．
由y(0)=0，y’(0)=1及上述递推公式，得
y^(2k)(0)=0，k=1，2，…；
y^(2k+1)(0)=(-1)^k(2k)!，k=0，1，2，…．