问题
问答题
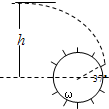
在我南方农村有一种简易水轮机,如图所示,从悬崖上流出的水可看作连续做平抛运动的物体,水流设计与下边放置的轮子边缘相切,水冲击轮子边缘上安装的档水板,可使轮子连续转动,输出动力,当该系统稳定工作时,可近似认为水的末速度与轮子边缘的线速度相同.设水的流出点比轮轴高h=5.6m,轮子半径R=1m.调整轮轴O的位置,使水流与边缘切点对应的半径与水平线成37°.(已知sin37°=0.6,cos37°=0.8,g=10m/s2),求:
(1)水流的初速度大小v0为多少?
(2)若不计档板的长度,求轮子转动的角速度为多少?
答案
(1)流出的水做平抛运动,设在空中运动的时间为t,则:
h-Rsinθ=
gt2 1 2
解得:t=
=2(h-Rsinθ) g
s=1s2×(5.6-0.6) 10
由合速度与分速度的关系有:
tanθ=
,v0 gt
解得:v0=7.5m/s
(2)设水与轮接触时的速度为v,则有:
v=
=12.5m/sv0 sinθ
设轮子转动的角速度为ω,由于水的末速度与轮子边缘的线速度相同
则有:ω=
=12.5rad/sv R
答:(1)水流的初速度大小v0为7.5m/s;
(2)若不计档板的长度,轮子转动的角速度为12.5rad/s.
