问题
单项选择题
设f（x）有连续的导数f（0）=0，f’（0）≠0，F（x）=
（x2-t2）f（t）dt，且当x→0时，F’（x）与x3是同阶无穷小，则k等于（）。
A.1
B.2
C.3
D.4
答案
参考答案：C
解析：
因为
，
所以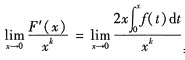
=
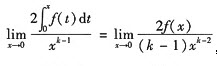，于是当k=3时，
，满足同阶无穷小的条件，故选C．
搜题请搜索小程序“爱下问搜题”
设f（x）有连续的导数f（0）=0，f’（0）≠0，F（x）=（x2-t2）f（t）dt，且当x→0时，F’（x）与x3是同阶无穷小，则k等于（）。
A.1
B.2
C.3
D.4
参考答案：C
解析：
因为，
所以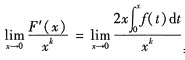=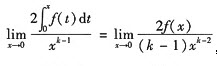，于是当k=3时，，满足同阶无穷小的条件，故选C．