问题
问答题
设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b)=1,证明:存在ξ,η∈(a,b)使得eη-ξ[f(η)+f’(η)]=1.
答案
参考答案:[证明] 构造辅助函数g(x)=ex,则g(x)在[a,b]上连续,在(a,b)内可导且g’(x)=ex.由拉格朗日中值定理,至少存在一点ξ∈(a,b),使
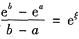 .
.
另作辅助函数F(x)=exf(x),F(x)在[a,b]连续,(a,b)内可导,由拉格朗日中值定理得,存在η∈(a,b),
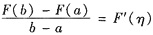 ,即
,即
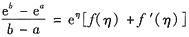 ,
,
从而有eη[f(η)+f’(η)]=eξ.即η-ξ[f(η)+f’(η)]=1.

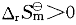 >0的是:()
>0的是:()