问题
计算题
（14分）如图所示，位于竖直平面上的1/4圆弧光滑轨道，半径为R，OB沿竖直方向，上端A距地面高度为H，质量为m的小球从A点由静止释放，最后落在水平地面上C点处，不计空气阻力，
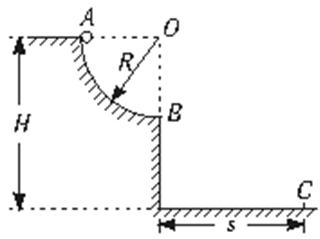
（1）小球运动到轨道上的B点时，求小球对轨道的压力为多大?
（2）求小球落地点C与B点水平距离s是多少?
（3）若轨道半径可以改变，则R应满足什么条件才能使小球落地的水平距离s最大？
答案
（1）3mg
（2）
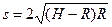
（3）当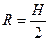
时，s最大
（1）小球由A→B过程中，根据机械能守恒定律有：
mgR＝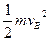
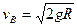
小球在B点时，根据向心力公式有；
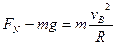
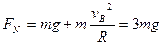
根据牛顿第三定律，小球对轨道的压力大小等于轨道对小球的支持力，为3mg
（2）小球由B→C过程，
水平方向有：s=vB·t
竖直方向有：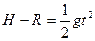
解得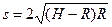
（3）水平距离：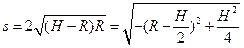
所以，当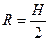时，s最大