问题
问答题
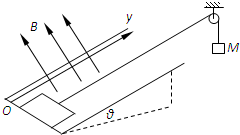
如图所示,一边长为L,质量为m,电阻为R的正方形金属框放置在倾角为θ的光滑绝缘斜面的底端,并用细线通过轻质定滑轮与质量为M的重物相连.磁场的方向垂直金属框平面,磁感应强度的大小只随y方向变化,规律为B=B0+ky,k为大于零的常数.假设运动过程中金属框总有两条边与y轴平行,且金属框不转动,当金属框沿y轴方向运动距离为h时速度达到最大.不计空气阻力,斜面和磁场区域足够大,重力加速度为g.求:
(1)金属框的最大速度;
(2)金属框从开始运动到达到最大速度的过程中,金属框中产生的焦耳热;
(3)金属框从开始运动到达到最大速度的过程中,通过金属框横截面的电量.
答案
(1)达到最大速度时,金属框及物体的加速度为零,
有:Mg=T
T=mgsin37°+F
F=(B2-B1)IL=KIL2
I=
=(B2-B1)Lvm R kL2vm R
解以上方程,可解得:
vm=(M-msinθ)gR k2L4
(2)设产生的焦耳热为Q,根据能量守恒定律,
有Mgh-mghsinθ=
(M+m)vm2+Q1 2
得:Q=(M-msinθ)gh-(M+m)(M-msinθ)2g2R2 2k4L8
(3)q=
△t=. I
△t=△φ △tR △φ R
△φ=△B•L2=khL2
解得:q=kL2h R
