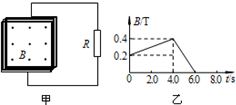
如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻R=4.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求:
(1)在t=2.0s时刻,通过电阻R的感应电流的大小;
(2)在t=2.0s时刻,电阻R消耗的电功率;
(3)0~6.0s内整个闭合电路中产生的热量.
(1)根据法拉第电磁感应定律,0~4.0s时间内线圈中磁通量均匀变化,产生恒定的感应电流.
t1=2.0s时的感应电动势E1=n
=n△Φ △t1 (B4-B0)S △t1
根据闭合电路欧姆定律,闭合回路中的感应电流I1=E1 R+r
解得 I1=0.2A
(2)在t=2.0s时刻,电阻R消耗的电功率P=I12R=0.16W.
(3)根据焦耳定律,0~4.0s内闭合电路中产生的热量
Q1=I12(r+R)△t1=0.8 J
由图象可知,在4.0s~6.0s时间内,线圈中产生的感应电动势E2=n
=n△Φ2 △t2 Φ6-Φ4 △t2
根据闭合电路欧姆定律,t2=5.0s时闭合回路中的感应电流I2=
=0.8AE2 R+r
闭合电路中产生的热量 Q2=I22(r+R)△t2=6.4J
故0~6.0s内整个闭合电路中产生的热量Q=Q1+Q2=7.2J.
答:(1)在t=2.0s时刻,通过电阻R的感应电流的大小为0.2A;
(2)在t=2.0s时刻,电阻R消耗的电功率为0.16W;
(3)0~6.0s内整个闭合电路中产生的热量为7.2J.
