某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元。
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少?
解:(1)设今年三月份甲种电脑每台售价x元,则去年三月份甲种电脑每台售价(1000+x)元,
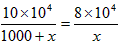 ,
,
解得x=4000,经检验x=4000满足题意,
∴今年三月份甲种电脑每台售价4000元;
(2)设进甲种型号电脑x台,则进乙种电脑(15-x)台,则
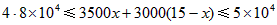
3000≤500x≤5000,
6≤x≤10,
又x为整数,
∴x=6,7,8,9,10,
∴共有5种进货方案;
(3)由(2)知获利为:(4000-3500)x+(3800-3000-a)(15-x)
=500x+(800-a)(15-x)
=12000+(a-300)x-15a,
∵要使(2)中所有方案获利相同,即获利与x无关,则
a-300=0,
∴a=300,此时所有方案获利均为7500元。
