问题
解答题
某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A队要多用10天,学校决定由三个工程队一齐施工,要求至多6天完成维修任务,三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍,这样他们至少还需要3天才能成整个维修任务。
⑴求工程队A原来平均每天维修课桌的张数;
⑵求工程队A提高工作效率后平均每天多维修课桌张数的取值范围。
答案
解:⑴设C队原来平均每天维修课桌x张,
根据题意得: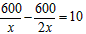 ,
,
解这个方程得:x=30,
经检验x=30是原方程的根且符合题意,2x=60,
答:A队原来平均每天维修课桌60张;
⑵设C队提高工效后平均每天多维修课桌x张,
施工2天时,已维修(60+60+30)×2=300(张),
从第3天起还需维修的张数应为(300+360)=600(张)
根据题意得:3(2x+2x+x+150)≤660≤4(2x+2x+x+150),
解这个不等式组得:3≤x≤14,
∴6≤2x≤28,
答:A队提高工效后平均每天多维修的课桌张数的取值范围是:6≤2x≤28。