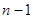平面内不过同一点的n条直线两两相交,它们的交点个数记作an,并且规定a1=0.那么:①a2=_____;②a3-a2=_______;③an-an-1=______(n≥2,用含n的代数式表示).
1,2,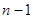
分析:n条直线相交,最多有1+2+3+…+(n-1)= 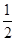 n(n-1)个交点.
n(n-1)个交点.
解答:解:①a2=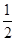 n(n-1)=1;
n(n-1)=1;
②∵a3=3,a2=1
∴a3-a2=3-1=2;
③an-an-1=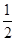 n(n-1)-
n(n-1)- 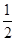 (n-1)(n-2)=
(n-1)(n-2)=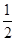 (n-1)(n-n+2)=n-1.
(n-1)(n-n+2)=n-1.
故答案为:1,2,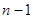
平面内不过同一点的n条直线两两相交,它们的交点个数记作an,并且规定a1=0.那么:①a2=_____;②a3-a2=_______;③an-an-1=______(n≥2,用含n的代数式表示).
1,2,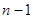
分析:n条直线相交,最多有1+2+3+…+(n-1)= 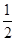 n(n-1)个交点.
n(n-1)个交点.
解答:解:①a2=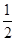 n(n-1)=1;
n(n-1)=1;
②∵a3=3,a2=1
∴a3-a2=3-1=2;
③an-an-1=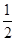 n(n-1)-
n(n-1)- 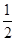 (n-1)(n-2)=
(n-1)(n-2)=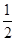 (n-1)(n-n+2)=n-1.
(n-1)(n-n+2)=n-1.
故答案为:1,2,