问题
解答题
某公司开发的960件新产品,需加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导。
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)该公司要选择省时又省钱的工厂加工,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,才可满足公司要求,有望加工这批产品。
答案
解:(1)设甲工厂每天加工x件,则乙工厂每天加工(x+8)件,
由题意得: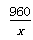 -20=
-20=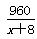
解之得:x1=-24,x2=16,
经检验,x1、x2均为所列方程的根,但x1=-24 不合题意,舍去,
此时x +8 = 24,
答:甲工厂每天加工16件,乙工厂每天加工24件;
(2)由(1)可知加工960件产品,甲工厂要60天,乙工厂要40天.所以甲工厂的加工总费用为60(800 + 50)=51000(元),
设乙工厂报价为每天m元,则乙工厂的加工总费用为40(m + 50)元,
由题意得:40(m+50)≤51000,解之得m≤1225,
答:乙工厂所报加工费每天最多为1225元时,可满足公司要求,有望加工这批产品。
