问题
计算题
（15分）
如图所示，一小球自平台上水平抛出，恰好落在临 * * 台的一倾角为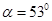
的光滑斜面顶端，并刚好沿光滑斜面下滑，已知斜面顶端与平台的高度差
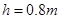，重力加速度
，
，
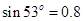，求
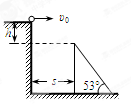
（1）小球水平抛出的初速度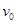
是多少？
（2）斜面顶端与平台边缘的水平距离s是多少？
（3）若斜面顶端高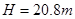
,则小球离开平台后经过多长时间t到达斜面底端？
答案
（1）vy = 4m/s，v0 =" 3m/s" （2）1.2m （3）2.4s
（1）由题意可知：小球落到斜面上并沿斜面下滑，说明此时小球速度方向与斜面平行，否则小球会弹起，所以vy = v0tan53°
vy2 =" 2gh"
代入数据，得vy = 4m/s，v0 =" 3m/s"
（2）由vy = gt1得t1 =" 0.4s"
s =v0t1 =" 3×0.4m" = 1.2m
（3）小球沿斜面做匀加速直线运动的加速度a =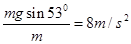 
初速度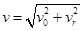
= 5m/s
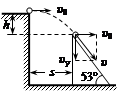
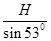=vt2 + 
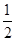at22
代入数据，整理得 4t22 + 5t2 - 26 = 0
解得 t2 =" 2s" 或t2 =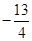 
s(不合题意舍去)
所以t = t1 + t2 = 2.4s
本题考查平抛运动规律的应用，根据沿斜面进入，可判断此时速度方向，把速度分解到水平和竖直两个方向，即可求得水平分速度和竖直分速度，在斜面由牛顿第二定律求出加速度，根据运动学公式求解
