[1]Not all parties have to be time-consuming and expensive to plan.It’s possible to have a party that’s simple but fun for everyone.Before you plan the party,it helps to write an outline of what kind of party you want to have,what foods and entertainment you’ll provide and so on.The following are tips on how to plan an excellent simple party.
[2]Choose a party theme that goes along with your interest and is easy to handle for you.If you’re a huge jazz fan and you have a large collection of jazz albums,build your party on a jazz theme.Visit local party supply stores and pick up music decorative items such as tablecloths,glasses,plates and napkins.
[3]Decide______available you have to spend on your party.Be practical about the length of time tasks are likely to take,such as how much time you spend on pre-party house cleaning,meal preparation and shopping for party materials.Add a time buffer(缓冲)into.your calculations.This way if anything goes wrong you will be able to deal with it.
[4]Prepare the food for your party.Make a trip to the store to get all your ingredients.Do this 2 or 3 days before the party as this will make sure all your ingredients are fresh and allow you to concentrate on meal preparation rather than running around searching for last-minute ingredients.Besides,you should make sure that if kids are part of the group,there are some delicious snacks for them.
[5]If you choose to hold it at home,make sure you have cleaned your home up and organized it at least a day or two before.Decorate the entrance hall or doorway to create a welcoming atmosphere.Make sure that the lighting is appropriate.Check the restrooms for extra toilet paper,tissue and soap.
小题1:What party themes should we choose?( no more than 12 words)
________________________________________________________________________
小题2:Fill in the blank in paragraph 3 with proper words.(no more than 5 words)
________________________________________________________________________
小题3:Why should we buy ingredients 2 or 3 days before the party?(no more than 12 words)
________________________________________________________________________
小题4:Complete the following statement with words from Paragraph4.(no more than 3 words)
Make sure to prepare some_____if there are kids in the party.
小题5:What does the underlined word“ it”in Paragraph 5 probably refer to?(no more than 2 words)
________________________________________________________________________
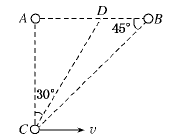
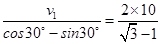m/s="27.3" m/s