如图所示，一个半径为R的光滑圆弧轨道APB竖直固定放置，PQ为其竖直对称轴，∠AOQ与∠BOQ都等于θ。现让一可看做质点的小球在轨道内侧运动，当其冲出A点后恰好可以从B点再进入轨道，所以此运动可以周而复始进行。已知小球质量为m，重力加速度为g，试求：
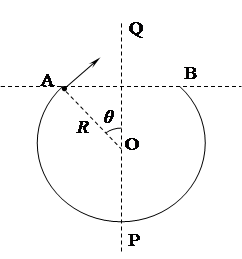
(1)小球离开轨道后的最高点距直线AB的距离；
(2)若要小球在最低点时对轨道的压力最小，θ应为多少？对应的最小压力为多少？
(1)h=
(2)Nm=
(1)物体刚刚冲出A点时，将物体速度分解有
v1=vcosθ (1)
v2=vsinθ (2)
在抛出到最高点过程中，水平方向为匀速直线运动，有
Rsinθ=v1t (3)
竖直方向为匀变速直线运动，末速度为零，时间逆向来看是初速度为0的自由落体运动，有
v2=gt (4)
h=
(5)
由以上(1)(2)(3)(4)可解得
v=
(6)
t=
(7)
由(5)得
h= (8)
(2)设物体在最低点的速度为v'，则物体在从A到最低点过程中，根据动能定理
mgR(1+cosθ)=
(9)
在最低点，由向心力公式，有
N-mg=
(10)
由(6)(9)(10)得
N=
(11)
分析知当θ=45º时，N最大为
Nm= (12)
评分标准：
(1)问6分，(3)(4)各2分，(5)(8)各1分。
(2)问6分，(9)(10)各2分，结果2分。
本题考查斜上抛运动规律，水平方向不受外力做匀速直线运动，竖直方向只受重力作用做竖直上抛运动，到达最高点时竖直分速度减小到零，先把初速度分解，由水平方向匀速运动求得运动时间，再由竖直方向的运动求得竖直分速度，由竖直上抛运动求得竖直高度，从抛出到最低点，由动能定理列出公式，在最低点，由支持力和重力的合力提供向心力，写出支持力的表达式，再由数学方法求得最大值