问题
解答题
(12分)设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
答案
(1)a的值为-1或-3;
(2)a的取值范围是a≤-3.
解:由x2-3x+2=0得x=1或x=2,故集合A={1,2}.
(1)∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0⇒a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件;
综上,a的值为-1或-3;
(2)对于集合B,
Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B⊆A,
①当Δ<0,即a<-3时,B=∅满足条件;
②当Δ=0,即a=-3时,B={2},满足条件;
③当Δ>0,即a>-3时,B=A={1,2}才能满足条件,
则由根与系数的关系得

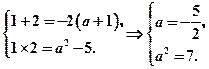 矛盾;
矛盾;
综上,a的取值范围是a≤-3.
