问题
计算题
（12分）质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动，细绳能承受的最大拉力Tmax=46N,转轴离地h=6m，g=10m/s2。
试求：（1）在若要想恰好通过最高点，则此时的速度为多大？
（2）在某次运动中在最低点细绳恰好被拉断则此时的速度v=?
（3）绳断后小球做平抛运动，如图所示，求落地水平距离x？
答案
（1）
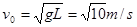（2）v=6m/s （3）x=6m
题目分析：（1）当小球恰好通过最高点时，小球只受重力。设此时速度为v0
故：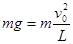
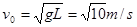(2分)
∴ （2分）
（2）小球在最低点受力如图所示，由牛顿第二定律得：
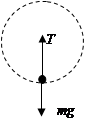
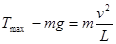， (2分)
代入数据得：v=6m/s （2分）
（3）细绳断后，小球做平抛运动，设水平距离为x
则有：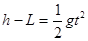
得：t=1s (3分)
x=vt 得x=6m （1分）
点评：本题难度较小，在最高点当绳子的拉力为零时，是小球通过最高点的临界条件，在最低点根据沿半径方向上的合力提供向心力求解