问题
解答题
已知集合A={x|a-1<x<2a+1}，B={x|0<x<1}，若A∩B=φ，求实数a的取值范围.
答案
a≤-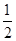 
或a≥2
题目分析：解：∵A∩B=Ø,
(1)当A=Ø时，有2a+1≤a-1⇒a≤-2;
(2)当A≠Ø时，有2a+1>a-1⇒a>-2.又∵A∩B=Ø，则有2a+1≤0或a-1≥1⇒a≤-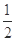 
或a≥2,∴-2<a≤- 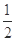或a≥2,
由以上可知a≤- 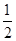或a≥2.
点评：集合有三种运算：交集、并集和补集。做此类题目，可结合数轴。