问题
计算题
如图甲，电阻为R=2
的金属线圈与一平行粗糙轨道相连并固定在水平面内，轨道间 距为d =0.5m，虚线右侧存在垂直于纸面向里的匀强磁场，磁感应强度为B1=0．1T，磁场内外分别静置垂直于导轨的金属棒P和Q，其质量m1=m2= 0．02kg，电阻R1=R2= 2．t=0时起对左侧圆形线圈区域施加一个垂直于纸面的交变磁场B2，使得线圈中产生如图乙所示的正弦交变电流（从M端流出时为电流正方向），整个过程两根金属棒都没有滑动，不考虑P和Q电流的磁场以及导轨电阻．取重力加速度g= l0m/s2，
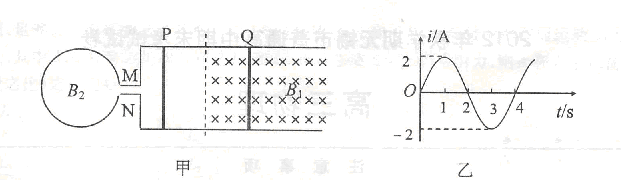
（1）若第1s内线圈区域的磁场B2正在减弱，则其方向应是垂直纸面向里还是向外？
（2）假设最大静摩擦力等于滑动摩擦力，金属棒与导轨间的滑动摩擦因数至少应是多少？
（3）求前4s内回路产生的总焦耳热．
答案
(1) 垂直纸面向里(2) 0.25．(3) 24J
题目分析：（1）第1s内线圈区域的磁场B2正在减弱，由图乙知：线圈中电流方向沿顺时针方向，根据楞次定律判断得知，磁场B2的方向垂直纸面向里．
（2）由图乙知，线圈中电流最大值为I0=2A，则通过Q棒的电流最大值为Im=1A;要使金属棒静止，安培力不大于最大静摩擦力，则有 B1Imd≤μmg
得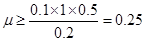 
，故金属棒与导轨间的滑动摩擦因数至少应是0.25．
（3）前4s内电流的有效值为 
回路的总电阻为R总=R+
=2Ω+1Ω=3Ω
回路产生的总焦耳热Q=I2R总t=24J