问题
选择题
如果A={x|ax2﹣ax+1＜0}=∅，则实数a的取值范围为（ ）
A．0＜a＜4
B．0≤a≤4
C．0＜a≤4
D．0≤a≤4
答案
答案：D
因为A={x|ax2﹣ax+1＜0}=∅，所以不等式ax2﹣ax+1＜0的解集是空集，
当a=0，不等式等价为1＜0，无解，所以a=0成立．
当a≠0时，要使ax2﹣ax+1＜0的解集是空集，
则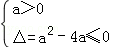
，解得0＜a≤4．
综上实数a的取值范围0≤a≤4．
故选D．