问题
计算题
如图,水平地面上有一转台，高h=10米，由半径为R=1米和r=0.5米的两个半圆柱拼合而成，可绕其中心轴转动，平台边缘上放有两个质量均为m=0.1kg的物体，可视为质点，由一根长为1.5m的细线连接在一起，且细线过转台的圆心，A、B两物体与平台接触面的动摩擦系数均为μ=0.2，最大静摩擦力等于滑动摩擦力。现在使转台转动的角速度缓慢地增大，g=10m/s2,求：
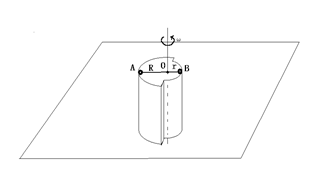
（1）在绳子无张力时，ω的最大值为多少？
（2）在A、B两个物体不滑动时，ω的最大值又为多少？
（3）接第2小题，当ω取最大值时，绳子突然断裂， A、B两个物体将同时离开转台，当两个物体同时第一次着地时，其着地点距离是多少？（结果带上根号）
答案
(1)
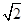rad/s (2) 2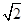rad/s (3) 
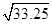m
题目分析：（1）绳子无张力，即向心力完全有静摩擦力充当，所以最大为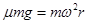
，所以A最先滑动，故不能超过A的最大角速度，为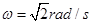
（2）当拉力超过B的滑动摩擦力时，两者发生滑动，所以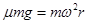可得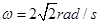
（3）两小球落地时间为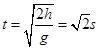
，A做平抛运动的速度为：
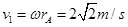，B做平抛运动的速度为：
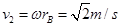，两者离开平台时的速度方向正好相反，所以相距距离为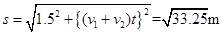
点评：本题的第三问，关键是知道相距的距离，是直径方向上的位移和平抛水平方向上的位移的矢量和
